問題15(直線図形)※サピックスオープン(中3)より
オリジナル問題
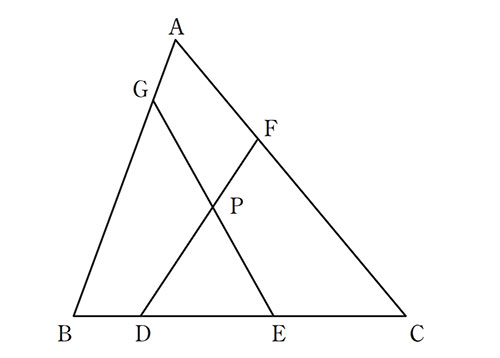
上の図のように,BC=10 で,面積が50である△ABCの辺BC上に,BD=2,CE=4 となる2点D,Eをとる。また,辺AC上に AF:FC=3:5 となるような点Fをとる。さらに,線分EGで△ABCの面積を二等分するように,辺AB上に点Gをとる。
DFとEGとの交点をPとするとき,次の各問いに答えよ。
- △ABC:△FDC を求めよ。
- AG:GB を求めよ。
- 四角形AGPFの面積を求めよ。
- 2016年度実施「サピックスオープン(中3)」より
作問者からのメッセージ
この問題では,小問ごとのつながりを意識して,分かったことを利用しながら解いていく力=分析力が求められます。序盤は単純な面積比の公式で解けますが,そこで得た事実を利用して,求めやすい図形に置き換えることで最後の小問の答えまでたどりつけます。
なお,これは2016年9月のサピックスオープンでの出題ですが,翌2017年のラ・サール高校の入試にて,設定が非常によく似た問題〔大問2(4)〕が出されています。あわせてチャレンジしてみてください。
他の問題にチャレンジしたい方へ
【志望校合格力判定付】公開模試にチャレンジしたい方へ
SAPIXの公開模試は、最新の入試動向を反映し、徹底した問題分析のもとに作られたオリジナル模試です。難関校に合格した数多くの卒業生のデータに基づき、母集団の変動に左右されない精度の高い志望校合格力判定と、合格に向けた学習指針を示します。
