小学生の算数で「数学の先取り学習」をしない理由
コラム
解説者:SAPIX中学部数学科 講師
中学範囲の先取りをするのは決して難しいことではありません。やろうと思えばSAPIX中学部でも問題なく行えますが、SAPIX中学部の小学生の算数カリキュラムでは先取り学習をしていません。
例えば高校受験の英語では、高校で学ぶ範囲の内容まで理解しておくと長文問題などを解きやすくなることが多いため、単語や文法の学習に“上限”がありません。学べば学ぶほど、それが得点につながるので先取りすることがメリットになります。
一方、数学では高校で学ぶ範囲の内容が出題されることはほとんどありません。“上限”が決まっているので、先取りすることのメリットが薄いのです。
また、短期間で解き方だけを詰め込んでも本質の理解にはつながりません。実際、小学生で方程式を解ける生徒もいますが、ほとんどの場合、移項の概念などは理解せずに単に解き方を知っているだけという状況です。高校受験において、解き方を知ることはもちろん大切ですが、「理屈を考えて理解する」ことがとても重要になります。
近年の高校入試の数学では、答えだけでなく考え方まで書かせる問題も増えており、「なぜそうなるのか」を示す証明問題も多くあります。これらの問題に対応するには、確固たる理屈が必要で、「なぜそうなるのだろう?」と考える習慣がとても大切です。
そして「理屈を考えて理解する」ためには長い時間をかけなければなりません。1回さらっとやっただけで「理屈も含めて完璧に理解しました!」という小学生はそういません。だからこそSAPIX中学部では、同じ単元に対してさまざまな角度からアプローチし、徐々に発展させるカリキュラムで何度も繰り返して学習するようにしているのです。
小学生が学ぶ範囲で「本質の理解」が必要になる例。皆さんは説明できますか?
35
÷
67
=
35
×
76
になる理由
-
35 ÷ 67 = 35 × 76 になる理由の解説はこちら
割り算にはそもそも「単位量あたり※の値を求める」という役割があります。
- 「単位量あたり」とは、「1m2あたり〇L」や「1個あたり〇円」などのような、「1(単位)あたりの量」のことを意味します。
分かりやすい例として「壁を3m2塗るのにペンキが6L必要」なときのことを考えてみましょう。この場合、1m2あたり塗るのに必要なペンキの量は6÷3=2(L)と割り算で求められますよね。
今回の計算を、上記のようなペンキの例に当てはめると、
「壁を67m2塗るのにペンキが35L必要。1m2あたりに必要なペンキの量は?」となります。これを解くにあたって、下の図で考えてみましょう。
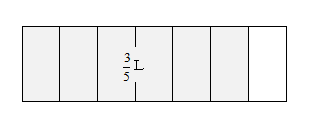
67m2とは、1m2の長方形の壁を7等分した6個分の大きさです。今回の問題は、この1m2の長方形全体を塗るのに必要なペンキの量を求めるということになります。
さて、これを見てどのように考えればよいか分かりますか?
きっと「7等分したうちの1個分の面積を塗るのに必要なペンキの量を求めて、それを7倍する」と考えた方が多いのではないでしょうか。
これを式にすると、「35(L)÷6(個分)×7」となります。
そして、この式の「÷6×7」の部分は順番を入れ替えて「×7÷6」とすることもできます。
さらに「7÷6」は76とすることができるので「35×76」となり、結果として「逆数を掛けた」形の式になるのです。
小学生で学習する内容がそのまま難関校の入試問題として出題されることも
高校受験で求められる、「理屈を考える」力を養うために必要な要素が小学校の算数にはたくさんあります。SAPIX中学部では、あえて先取り学習をせずにそれらを丁寧に扱っています。
実際、小学生で学ぶ「比」や「割合」の考え方は、高校入試問題においてもそのまま利用されることが多くあります。2023年の入試問題でお示しするならば、慶應義塾高校の大問1(7)です。この問題と、SAPIX中学部の小6の9月で扱っている内容(下図)はほぼ同じです。
-
SAPIX中学部の小学6年生用テキストより。類似問題が2023年慶應義塾高校の入試問題で出された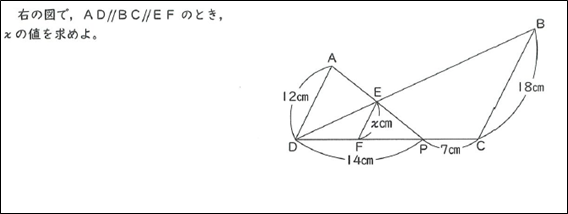
このように、小学生で学習する内容がそのまま難関校の入試問題として出題されることもよくあります。「比」や「割合」といった重要単元を、小学生の時期に徹底的に学習することは受験対策としても非常に意味があります。
「量感」や「数字感覚」をイメージで身に付けられるのが算数
小学生の算数は「量感を学ぶ」「ある物事に対する数字感覚を身に付ける」にはうってつけであり、その後の数学へ進む上でもじっくり学ぶ意味があると考えます。
例えば、「リンゴ5個で1000円」という言葉を聞いて、「重さ」「その値段が高いのか安いのか」「何人で食べられるか」「日持ちはどのくらいか」など、どれだけ多様な数字を思い浮かべられるか、ということが量感です。また、それを正確に、必要な情報だけをイメージできることも重要です。算数でロジカルな思考力と量感を身に付けられれば、見通しを立てるのもうまくなります。
一例として、課題が多めに出たときのスケジュールを考える際のプロセスを挙げてみます。
- 課題の量が先週より多そうだ……
- どのくらい多い? 普段の1.2倍くらいかな?(比や割合の概念で「量感」)
- 先週より1時間くらい長めに時間をとればいいかな?(物量を時間という別の量感に換算)
- そのためには、○日の□時から勉強しなきゃ!
このようにさまざまな条件を考えて、逆算して行動を整えていきます。時間の量感や学習内容の負荷の量感が分かっているほど正確に、早く、効率良く見通しを立てることができます。
こういったことを学ぶには、焦って先取りするよりも「イメージがつくものをより膨らませる」勉強法が適しています。だからこそ、小学生のうちは算数をじっくりと学ぶことが大切といえます。
「一次関数」でそれまでの学習姿勢の差が歴然となる
数学は「未知の問題を解決する方法を学ぶ教科」です。問題に向き合うとき、解法を当てはめながらもいったん立ち止まり、自分の知っている知識の原理を考え直し(一般化し)、どのように活用するかを考えることが必要な場面が多くあります。その最初のタイミングは中学生の「一次関数」です。
算数を単なる問題を解くツールとしてしか認識していなかった生徒は、中1の12月ごろに「一次関数」を学習すると、「なぜそういう式になるのか」といったことを考える習慣がないので、「全く分からない! やり方を教えて!」となってしまいがちです。
そこでSAPIX中学部では、題材としては算数を使いながらも深いところまで掘り下げることによって、小学生のうちから抽象的な内容を理解することにも慣れてもらっています。算数で「具体→抽象」のイメージトレーニングを積んできた生徒は、中学になってから数学で求められる「抽象→具体」の変換もスムーズに行うことができます。
一度身に付いた学習姿勢を改善することは本当に大変です。中学生になると、英語の学習も本格化しますし、部活や生徒会活動など中学校生活もとても忙しくなります。また、中1、中2と進むにつれ学ぶことの難度が上がってどんどん抽象化されていきます。
そのときに
- 「なぜそうなるのか」と考えること
- 数をイメージとして捉えること
といった正しい学習姿勢を早いタイミングで身に付けておくことはとても重要です。
算数と数学の違い
文部科学省が告示する「学習指導要領」によれば、算数は「普段の生活で活用できるような計算力、計算の正確さ」を向上させることを目標としています。つまり、解答を得ることを重視しています。
一方、数学は「物事を数学的な観点で考え、表現し、判断する力」の向上を目標としていて、解答よりもその過程やプロセスを重視してます。
その違いが中学で学ぶ範囲で最初に顕著に表れるのが、中1で学ぶ「一次関数」なのです。
算数は楽しんで学ぶことで学力がどんどん伸びていきます
「なんでだろう? どうしてだろう?」と考える大前提は、その内容に興味を持つことです。そのためにも、小学生の間は「楽しく学ぶ」ことが最も大切です。「やれるぞ! できるぞ! 楽しいぞ!」と思うと生徒は頑張る一方で、無理だと思ったら簡単に諦めてしまうことがあります。難しい言葉を使わずに、適切な分量で、楽しみながら学ぶことで、少しずつ階段を上ってもらい、ふと振り返ったら「あれ10段も上っているや」と思ってもらえるのが理想です。
算数や数学は、それ単体で実生活の役に立つことはあまりないと思います。三平方の定理や、文字式を実生活で使うことはないでしょう。ただ、「物事の本質や根幹をなすものは全て数学だ」と考えています。
例えば、完全に文系と思われている「心理学」の勉強をしたいという人には統計学が必要で、統計学を学ぶには、一次関数や微積分などの数学の根本理解が必須です。これを立ち返ってみると、小学校の算数からスタートになるわけです。
もう少し身近な例で考えると、「ある事柄を人に分かりやすく伝えるにはどうしたらよいか。図を使うとよいのか、一般化や抽象化したほうが良いのか」などを考える際の、論理的な思考も算数や数学から学べます。こういったことからも、物事の基本は全て算数・数学なのだと思うのです。

高校受験に向けて頑張る小学生と保護者の皆さまと、中学受験をするか迷われている方々へ
成長には個人差があります。中学受験は12歳での完成度が問われるため、どうしても成長がゆっくりな生徒には不利になります。それが15歳を迎える頃になると、ある程度成長度合いがそろってくるため、努力が結果となって現れやすくなります。また、自分のやりたいことや将来の目標も見え始める生徒も増えてきますので、より良い進学先を選べる確率も上がります。中学からの募集がなく、高校からの募集のみという私立校(※)もあります。さまざまな可能性や適性を見極めながら受験する学校を考えられる、というのが高校受験をするメリットといえるでしょう。
また、中学受験と高校受験の違いは「子どもと一緒に親も頑張る」のか、「子どもが頑張るのを親がサポートする」のかという点だと思います。大学入試になると、「全部子どもが頑張る」になるので、そこへ向けての成長の過程を一緒に歩める、成長の糧となるというのが、高校受験の良いところだといえるでしょう。私たちも、頑張る生徒たちをしっかりサポートしていきたいと思っています。
※ 高校募集のみの私立校の例
- 早稲田大学本庄高等学院
- 中央大学杉並高校
- 国際基督教大学(ICU)高校
